Lightweight Design of Large-tonnage Elevator Car Frame
-
摘要:
为提高大吨位电梯轿架的力学性能,实现轿架结构减重的目的,文中通过ANSYS Workbench平台建立参数化轿架模型,进行静载、动载力学分析以及模态分析,采用变密度法对轿底底架和拉杆建立拓扑优化模型,并基于拓扑优化结果对原轿底底架和拉杆的结构布局进行重构。然后,以轿架结构的总质量最小为优化目标,以构件标准参数的取值范围和轿架的最大变形值为约束条件,构建轿架构件尺寸优化模型。为提高求解速度,针对钢截面提出一种离散型参数拟合设计方法,并对轿架构件参数进行装配尺寸关联,依据参数拟合提出选型设计,完成优化求解后的参数选型。结果表明:优化后的轿架结构达到了轻量化的设计要求,并且满足安全性需求和各项力学性能指标。
Abstract:In order to improve the mechanical properties of large-tonnage elevator car frame and further reduce the weight of the car frame structure, a parametric car frame model is established by ANSYS Workbench. The static load & dynamic load analysis and modal analysis are carried out. The topology optimization model of the bridge bottom frame and pull rod is established with variable-density method. Based on the topology optimization results, the structure layout of the original bridge bottom frame and pull rod is reconstructed. Then, taking the minimum total mass of the car frame structure as the optimization objective and the value range of the standard parameters of the component and the maximum deformation value of the bridge as the constraint conditions, the size optimization model of the bridge frame is constructed. In order to improve the solving speed, a discrete parameter fitting design method is proposed for the steel cross-section, the parameters of the car frame are related to the assembly size and the selection design is proposed according to the parameter fitting. The parameter selection after optimization is completed. The results show that the optimized car frame structure can meet the design requirements of lightweight, safety requirement and the mechanical performance index.
-
引 言
目前,大吨位电梯[1]的垂直运输常配以叉车的水平搬运,促成厂房及生产线向空间发展,因此轿架结构的强度和刚度成为电梯设计考虑的主要因素。在传统的电梯设计过程中,为了使承载结构的强度和刚度满足要求,设计的承载结构质量会很大,轿架本身的质量在设计承载载荷中占相当大的比例[2]。轿架的质量过大,不仅会增加其制造成本,而且会使电机的曳引力大部分消耗在自重上面,导致电梯的有效搬运载荷减少及整体运输效率下降[3]。因此,在满足强度和刚度可靠性的前提下,需有效地优化货梯的承载结构,使货梯质量变小,达到减少能源消耗、降低制造成本的目的[4]。
在结构轻量化领域,国内外学者主要是对多工况载荷下的结构进行有限元分析[5-7],对不满足技术指标的结构采用拓扑优化、尺寸优化等方法进行优化设计,从而实现轻量化。在电梯结构优化方面,主要通过经验法、拓扑优化等,解决电梯变形和应力集中的问题,在结构轻量化和电梯结构优化方面已经取得了很好的效果,但针对大吨位货梯的相关研究仍较匮乏。
针对以上问题,本文以初步设计的5 t货梯为研究对象,从货梯轿架的结构需求出发,利用有限元分析和优化设计理论对货梯轿架进行结构轻量化技术研究。
1. 轿架模型构建
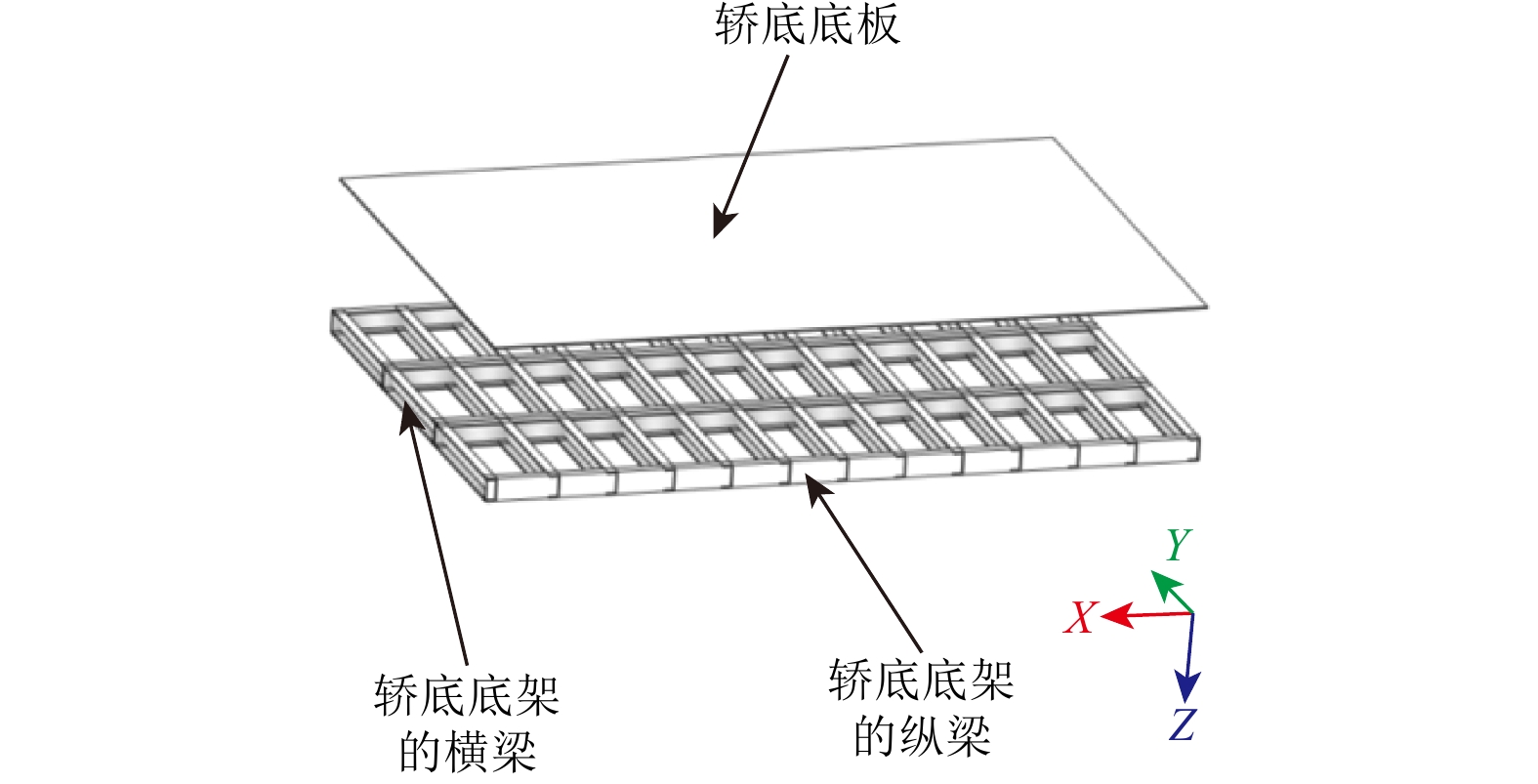
在建立轿架三维模型时,为确保有限元分析既准确又高效,需对电梯轿架进行简化。由于本文主要研究在各种工况下货梯承载部件的承载能力,因此只对承载部件进行分析。螺栓、螺母等连接件的相对体积较小,主要起连接作用,且它们的接触面积较小,只在局部产生集中应力,对整体构件并没有太大影响,因此不对这些连接件进行三维建模。此外,也不对导向轮、安全钳、导靴等部件进行建模,因为不需要分析导向轮、安全钳、导靴等结构内部的受力情况,只去除这些部件有利于减少计算量和避免计算结果不收敛的部分[8]。导向轮、安全钳和导靴起到的限位和约束作用在有限元分析中等效施加,保留其在实际中起到的作用。
2. 货梯轿架力学分析
通过对轿架模型的静载、动载和模态分析,判断构件的强度和刚度是否满足要求,为货梯轿架的拓扑优化提供优化目标。该货梯使用的槽钢、拉杆和轿底底板的材料均为Q235,模型的材料属性见表1。
表 1 Q235材料属性密度/(kg·m−3) 屈服极限/MPa 杨氏模量/GPa 泊松比 7 850 235 210 0.3 根据电梯制造标准,不同工况下选取的不同安全系数ns≥1.5。文中静载分析安全系数取3.0,动载分析安全系数取1.5;标准构件的刚度指标小于等于L /1 000(L为构件长度),因此对应的强度指标在静载分析时取78.3 MPa,在动载分析时取156.7 MPa。
在ANSYS Workbench中构建了由梁单元和壳单元组成的参数化轿架模型。对轿架进行超载、偏载、极限偏载三种工况的静力学分析,冲击载荷、安全制停两种工况的动力学分析以及模态分析。其中模态分析以及超载、偏载、极限偏载和冲击载荷工况下的约束条件为:在导向轮所在的上梁部位采用位移约束,其中Z向(货梯垂直运行方向)设置为0,X向和Y向自由移动;在导靴所在的直梁端部采用位移约束,其中X向和Y向(货梯水平方向)设置为0,Z向自由移动。安全制停工况下的约束条件为:在安全钳所在的中间直梁的下端部施加固定约束,在导靴所在的两侧直梁端部施加X向和Y向的位移约束。通过上述约束条件的合理设置,确保了模型在不同工况下的力学行为能够准确反映实际运行状态,为后续优化设计提供了可靠的仿真基础。
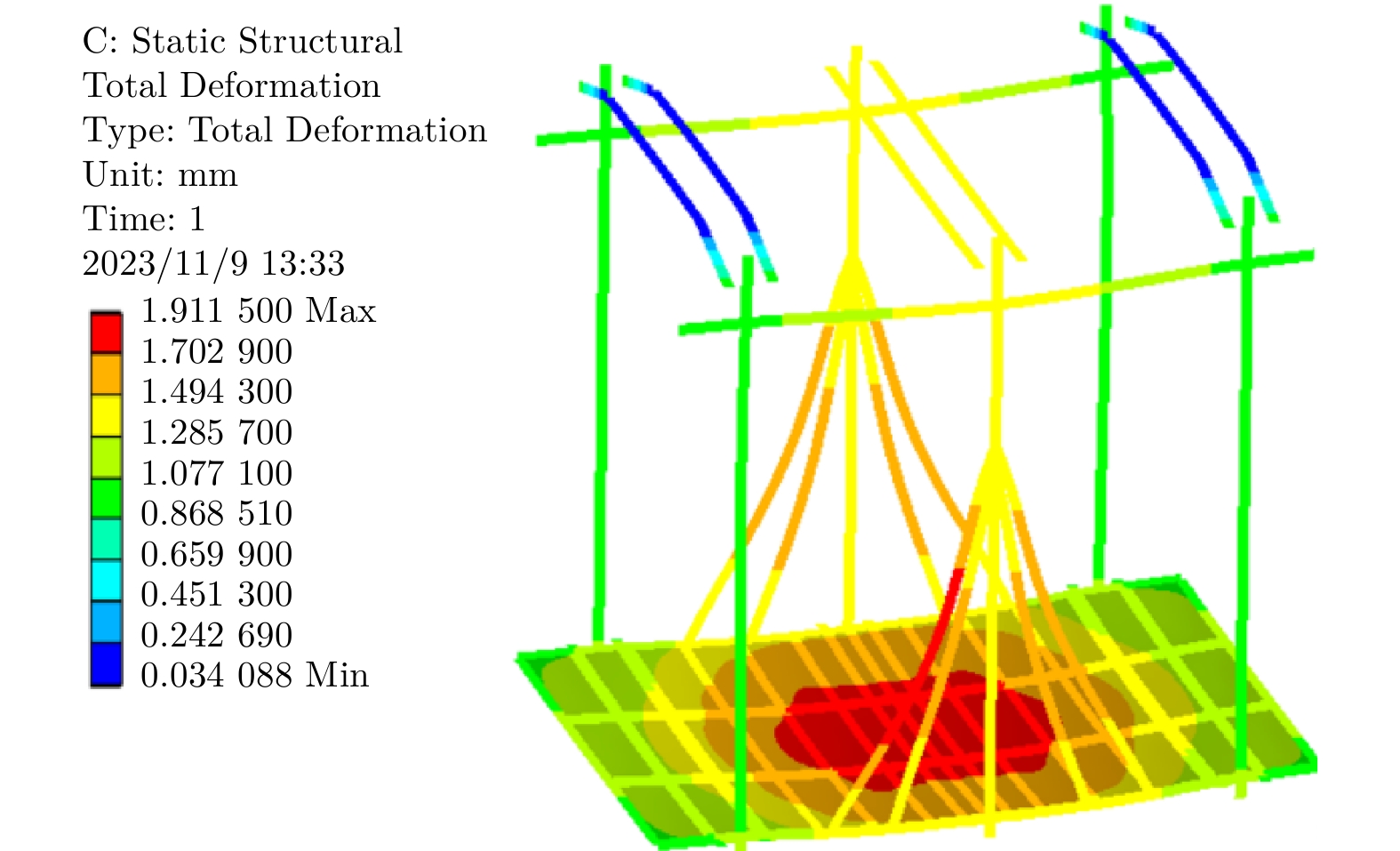
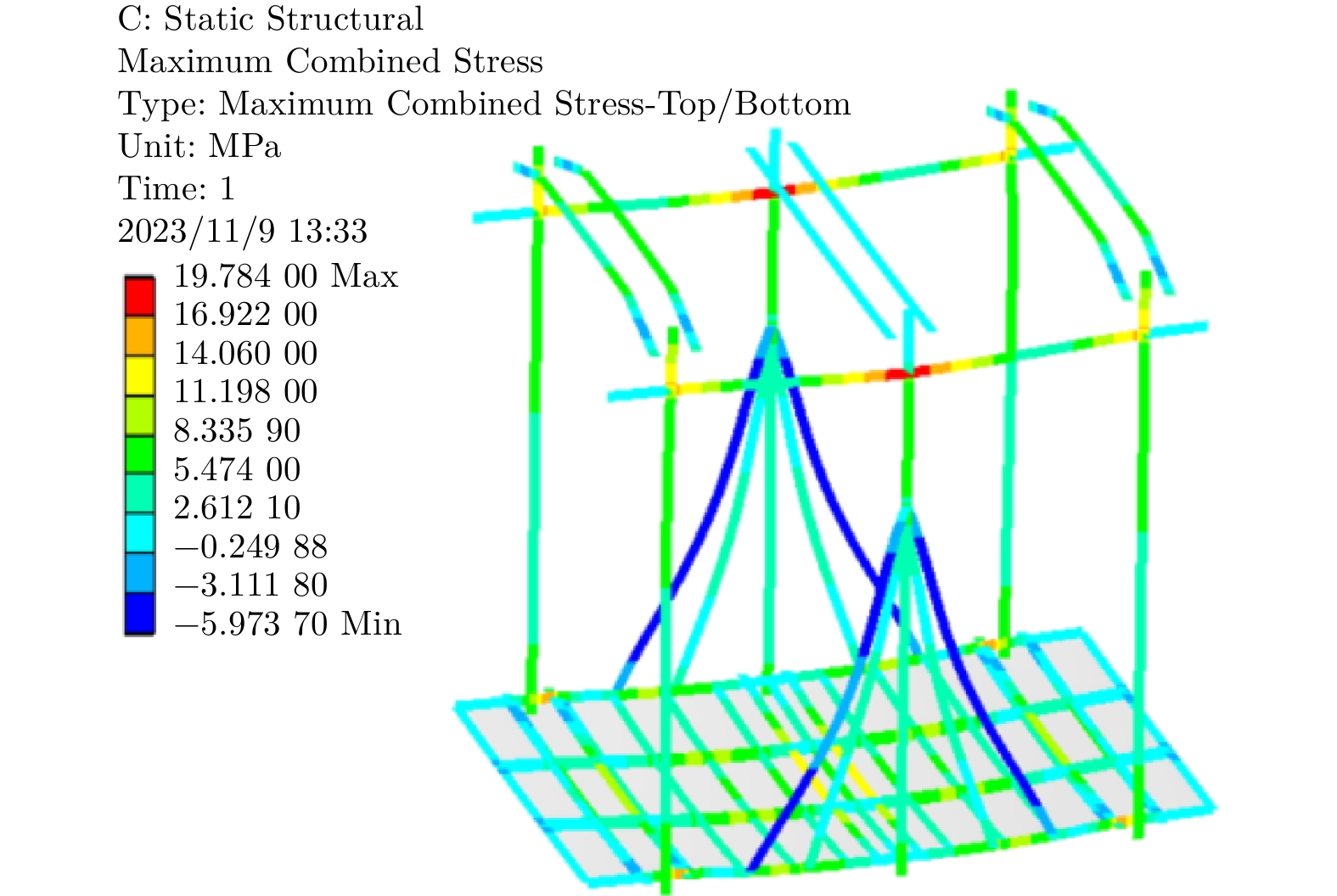
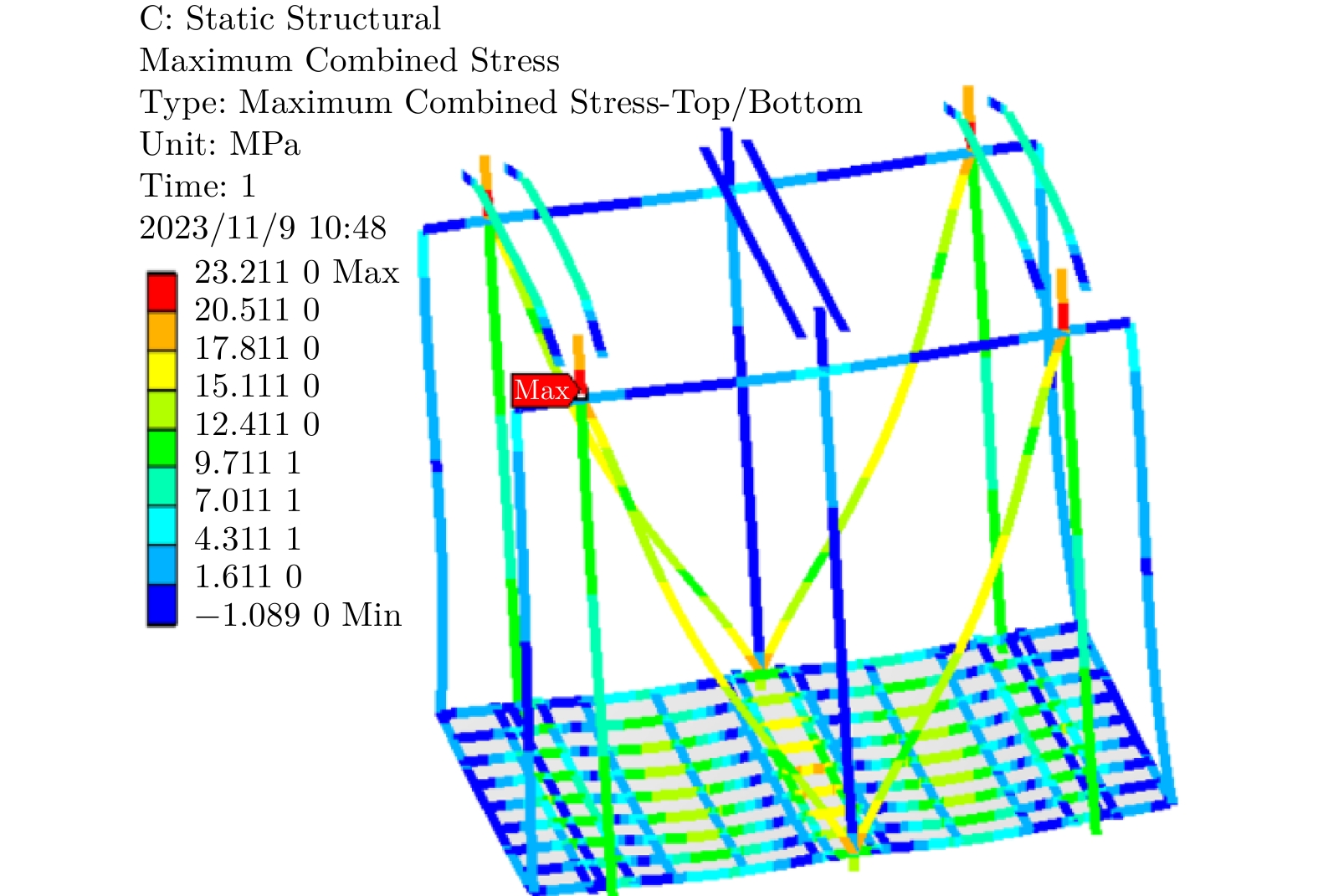
在超载工况下,将货梯125%的额定载重以力的方式(62 500 N)均匀施加在轿底底板上;在偏载工况下,将货梯的额定载重(5 t)以力的方式均匀施加在X/Y方向3/4的轿底底板面积上;在极限偏载工况下,将货梯80%的额定载重以力的方式均匀施加在入口处的轿底底板20%的面积上;在冲击载荷工况下,将货梯150%的额定载重以力的方式均匀施加在轿底底板上;在安全制停工况下,对轿架施加随时间变化的加速度。超载分析变形云图和应力云图如图3及图4所示,轿架力学分析结果见表2。
表 2 力学分析结果工况 最大
变形量/mm最大
应力 / MPa最大应力位置 超载 1.910 19.780 直梁和连接件连接处 偏载 1.870 20.690 直梁和连接件连接处 极限偏载 1.967 14.898 直梁和连接件连接处 冲击载荷 2.610 6.510 直梁和连接件连接处 安全制停 2.198 23.860 直梁和连接件连接处 由表2可知,在125%超载工况下的最大变形量和应力值分别为1.910 mm和19.780 MPa。经分析,最大应力出现在直梁和直梁连接件的连接处,最大变形出现在轿底底架和轿底底板上。如表3所示,模态分析中前两阶的模态最大变形量分别为5.224 mm和16.160 mm,最大变形均发生在拉杆部位。综上所述,拉杆和轿底底架的变形较大但均满足强度、刚度条件,各构件应力远小于相应材料的屈服强度,在改善拉杆和轿底底架结构的基础上,可进行轻量化设计。
表 3 六阶模态参数信息阶次 频率/Hz 变形/mm 1 13.284 5.224 2 13.989 16.160 3 13.999 16.940 4 14.076 16.900 5 14.078 18.810 6 14.090 16.600 3. 货梯轿架拓扑优化
3.1 拓扑优化数学模型的建立
建立轿架拓扑优化的数学模型采用的是变密度法[9],将结构的柔度值作为优化目标,以质量分数为约束条件,以单元的伪密度值为设计变量,故轿架拓扑优化的数学模型为:
\left\{ {\begin{array}{*{20}{c}} {{\text{find }}{\boldsymbol{X}} = {{({x_1},{x_2},{x_3}, \cdots ,{x_N})}^{\text{T}}} \in {{{\mathrm{{\boldsymbol{R}}}}}}} \\ {\min {\text{ }}f({\boldsymbol{X}}) = \displaystyle\sum\limits_{i = 1}^N {{\boldsymbol{u}}_i^{{{\mathrm{T}}}}{k_i}{{\boldsymbol{u}}_i}} } \\ {{\text{s}}{\text{.t}}{\text{. }}V{{(}}{\boldsymbol{X}}{{)}} \leqslant \theta {V_0} = \displaystyle\sum\limits_{i = 1}^N {{x_i}{V_i}} } \\ {{\boldsymbol{KU}} = {\boldsymbol{F}}} \end{array}} \right. (1) 式中:X和xi分别为N个单元的伪密度矢量和第i个单元的伪密度值([0,1]区间); {\mathrm{{\boldsymbol{R}}}} 为实数集;f(X) 为结构静态刚度目标函数;V(X)和Vi 分别为体积的约束函数和单元体积;V0为单个单元的体积;θ为体积约束值([0,1]区间);U和ui 分别为结构位移矢量和单元位移矢量;K和ki 分别为结构刚度矩阵和插值后的单元刚度;F 为载荷矢量。
3.2 轿底和拉杆拓扑优化分析
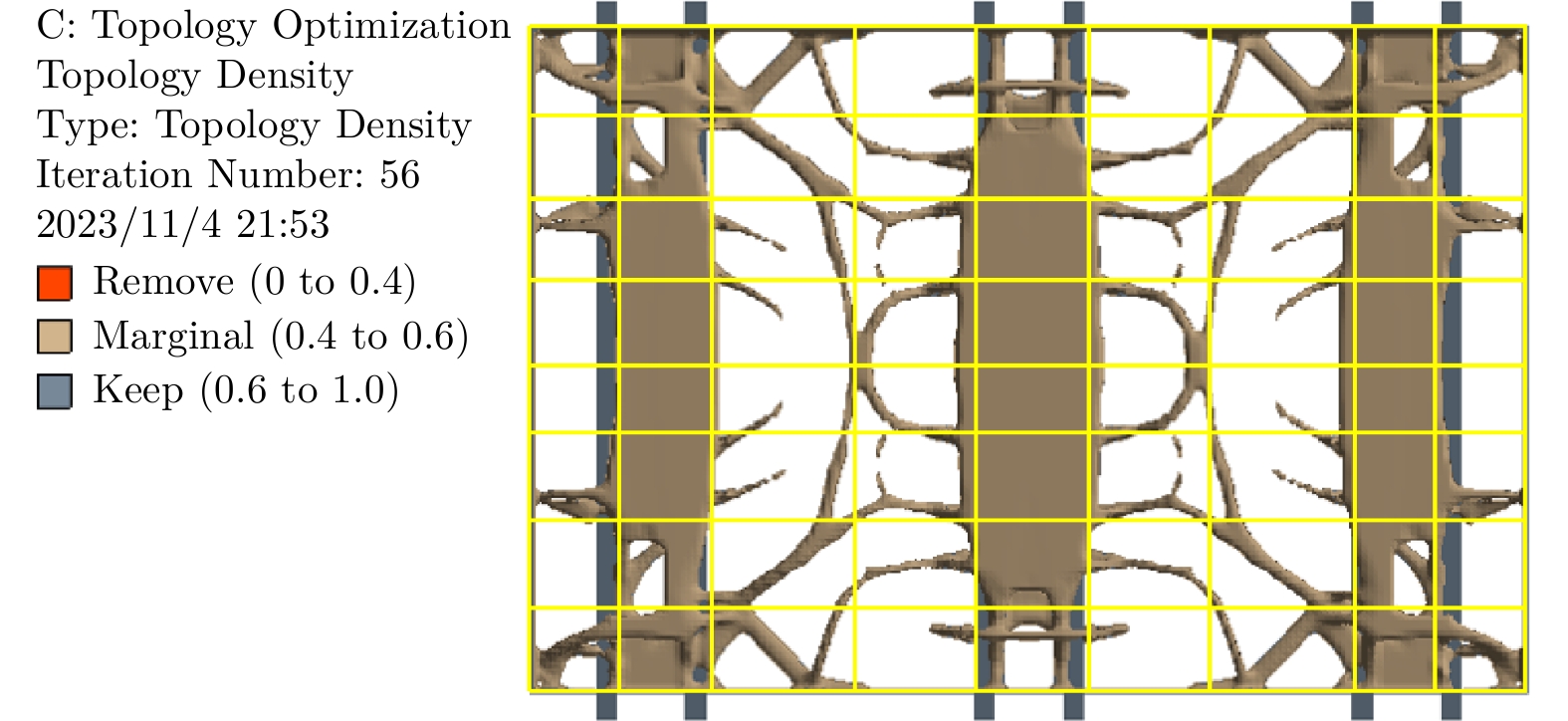
轿底底架拓扑优化[10]的模型由轿底底架填充区和下梁组成。根据模型的组成及其结构特点,在ANSYS中首先将轿底底架和下梁的网格划分尺寸分别设置为20 mm和6 mm,对轿底和下梁采用扫掠法划分网格,使其得到六面体网格,再采用Bond接触方式连接轿底底架填充区和下梁,最后划分出491 418个单元,690 696个节点。主要载荷类型为满载,因此在轿底拓扑优化中施加与超载工况相同的载荷条件。
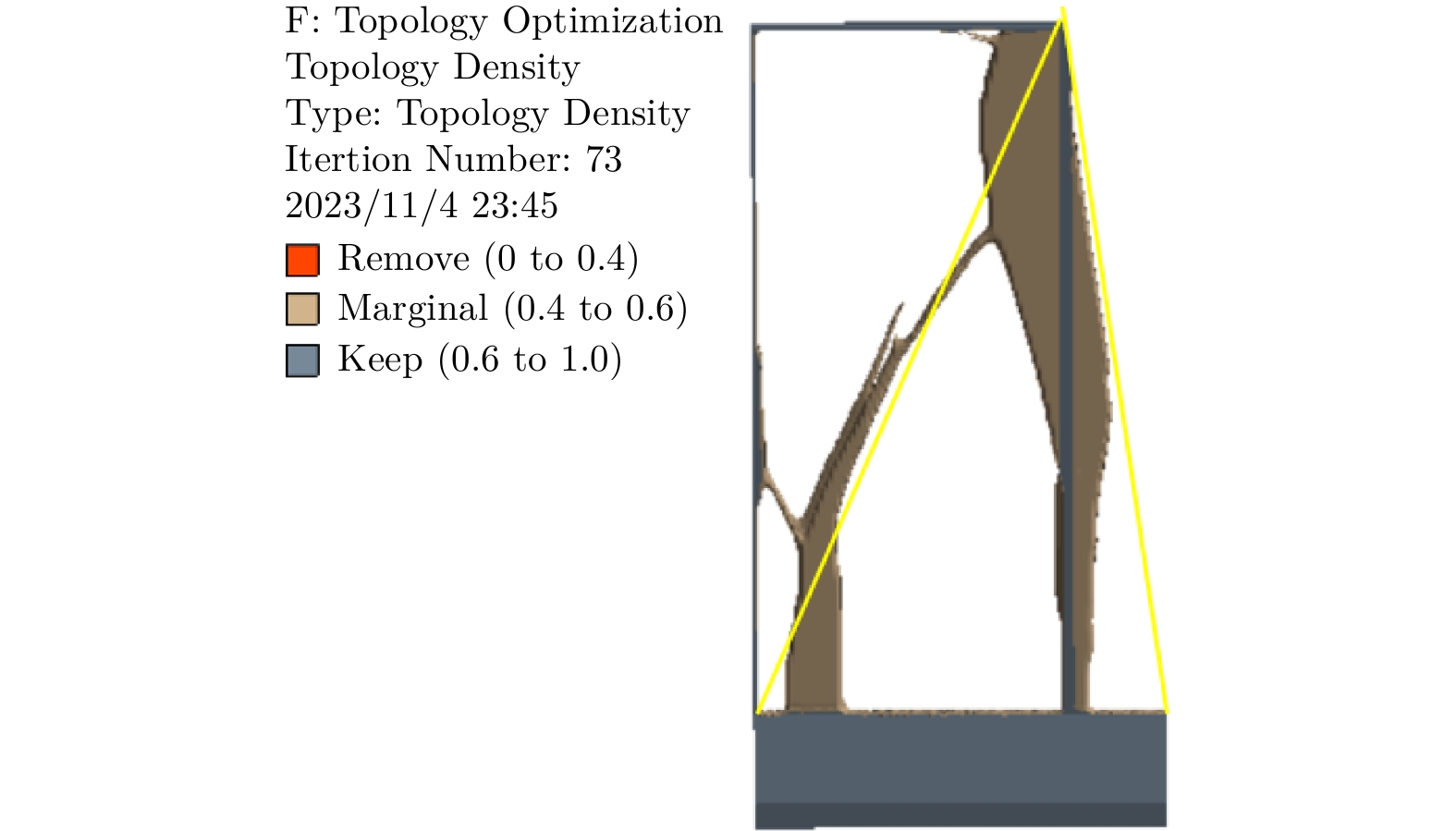
在ANSYS中设置约束条件和目标函数,创建设计响应Compliance表示结构的柔度值,同时创建整个模型质量分数的约束响应。约束条件是原模型质量0.2倍的质量分数,代表设计区域内变量达到其0.2 倍质量后停止收敛。根据已施加的满载边界条件进行力学分析,得出拓扑优化结果,再以梁单元的线框图走线(黄色线)代替实体单元的均匀分布,如图5所示。
拉杆拓扑优化的模型由轿底和拉杆填充区域组成,为了减少拓扑优化的计算量和计算时间,只选择其中的1/4模型作为拓扑优化的对象,相关的边界条件也进行相应的对称处理以减少计算量和计算时间。首先将整个模型的划分尺寸设置为20 mm,对整个模型自动划分网格,使其得到六面体网格,再采用节点耦合的接触方式连接不同的构件,最后划分出79 447个单元,76 229个节点。
对叉车搬运工况下在轿底门口处的集中载荷(大吨位货梯常遇到)进行静力学分析时,拉杆的拓扑优化需要考虑偏载和叉车搬运两种工况,因此对轿底填充区分别施加偏载和叉车载荷进行求解。其拓扑优化与轿底的拓扑优化相同,最后以梁单元的线框图走线(黄色线)代替实体单元的均匀分布,如图6所示。
3.3 轿架模型重构
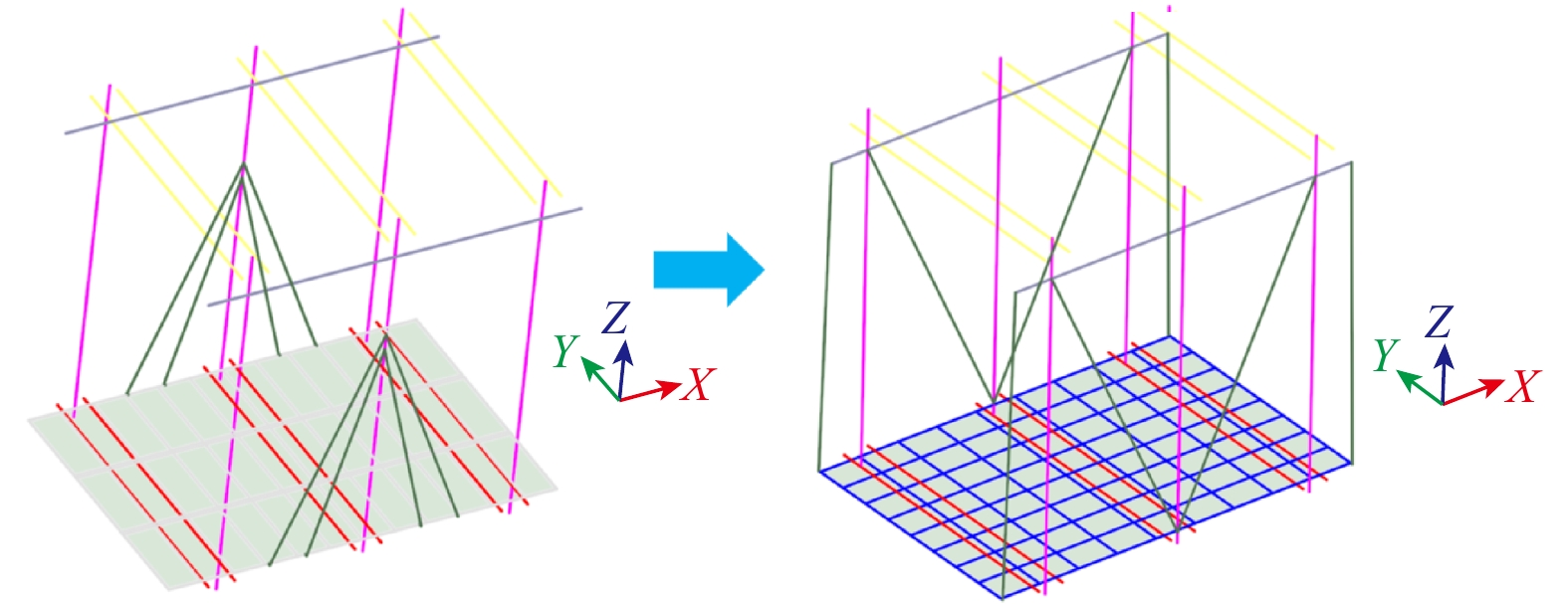
根据轿底和拉杆的拓扑优化结果,在原有轿架基础上对轿底和拉杆进行结构的重新设计和布置。原有轿底构件由槽钢组成,拉杆是半径为r的圆钢。为了不增加购买其他型材的成本,重新设计的轿底组成构件依旧为槽钢,栏杆依旧为圆钢,只是对应的尺寸发生了变化。原轿架梁单元模型重构如图7所示。
4. 离散型货梯轿架构件尺寸优化
4.1 尺寸优化数学模型建立
优化设计问题[10]是计算在规定的范围内由一系列可变基本参数构成的等式的预期值。等式是优化设计中的目标函数,构成等式的可变基本参数是优化设计中的设计变量,在规定的范围内是优化设计中的约束条件,故货梯轿架构件尺寸优化设计的数学模型为:
\min f({\boldsymbol{y}}) = f({y_1},{y_2}, \cdots ,{y_n}) (2) {\boldsymbol{y}} = \left[ {{y_1},{y_2}, \cdots ,{y_n}} \right] (3) \left\{\begin{split}& h_j({\boldsymbol{y}})=0 & (j=1,2, \cdots, p) \\& g_k(\boldsymbol{y})=0 & (k=1,2, \cdots, q) \\& y_i^{\mathrm{L}} \leq y_i \leq y_i ^{\mathrm{U}} \end{split}\right. (4) 式中:f(y)为尺寸优化目标函数,y为设计变量;g(y)为不等式约束函数;yi为货梯轿架的构件尺寸;h(y)为等式约束函数;上角标L为下限,上角标 U为上限。
4.2 槽钢截面尺寸参数拟合及选型设计
轿架主要部件全部采用槽钢(标准件),槽钢有A,B,C三种型号。本文的模型以Q公司的轿架模型为基础,槽钢型号为B型,所以在软件中将B型槽钢的高度h、 腿宽b、腰中间厚度d、腿中间厚度t中的一个参数作为变量,另外几个参数与该参数进行拟合,最终得出以下结果:
\left\{\begin{split}& b=0.19 h+31.1 \\& d=0.021 h+3.8 \\& t=0.028 h+5.5 \end{split}\right. (5) 参数拟合完成之后,参数由原来的32个减少到7个,不仅减少了计算量及计算时间,结果还可直接作为选型的依据。
为使整体优化后的轿架模型在满足最大有效面积的同时能满足强度和刚度的要求,本文只针对轿架构件中的槽钢截面参数进行优化,只是槽钢截面的参数优化后,原来构件之间的装配关系会发生改变。因此,对主要构件之间的装配尺寸进行关联设置,以确保满足轿厢最大有效面积和求解精度。
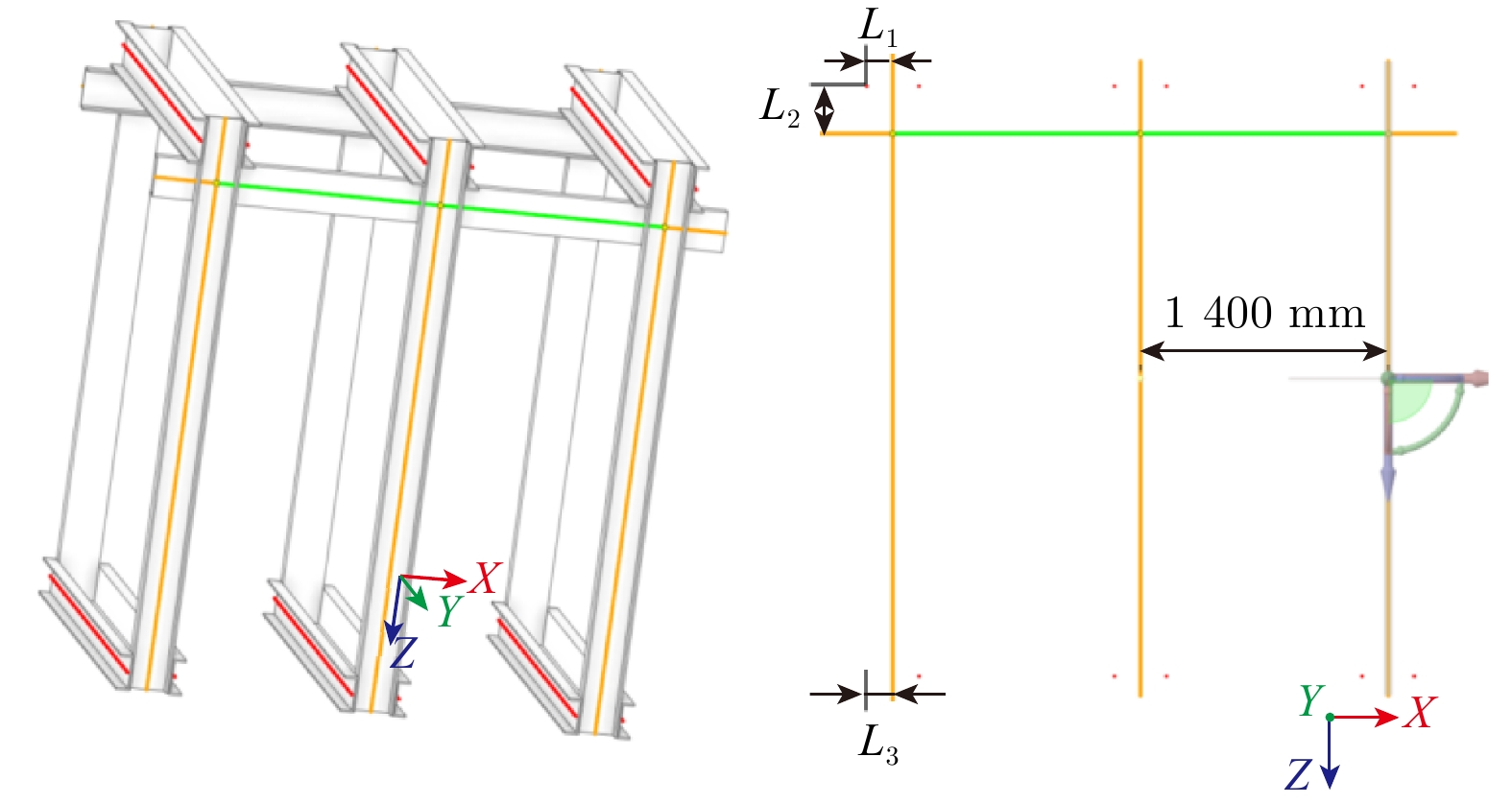
不更改直梁的位置,对上梁与直梁、下梁与直梁、直梁连接件与上梁进行装配尺寸设置,如图8所示。图中L1为上梁与直梁装配参数,L2为直梁连接件与上梁装配参数,L3为下梁与直梁装配参数。上梁槽钢高度为h1,直梁槽钢高度为h2,直梁连接件槽钢高度为h3,那么装配参数之间的关系如下:
\left\{\begin{split}& L_1=\frac{1}{2} h_2 \\& L_2=\frac{1}{2}\left(h_1+h_3\right) \\& L_3=\frac{1}{2} h_2 \end{split}\right. (6) 4.3 轿架模型构件尺寸的直接优化
由于文中的轿架结构优化设计只针对单一的超载工况分析,所以选择自适应单目标法。设定轿架的设计变量、约束条件、目标函数的数学模型为:
\left\{ {\begin{array}{*{20}{c}} {\min f(P) = f({p_1},{p_2}, \cdot \cdot \cdot ,{p_7})} \\ {{\text{find}}\,P \in {{\text{R}}}} \\ {\begin{array}{*{20}{c}} {{\text{s}}{\text{.t}}{\text{.}}}&{40 \leqslant {p_1}, \cdot \cdot \cdot ,{p_5} \leqslant 400} \end{array}} \\ {8 \leqslant {p_6},{p_7} \leqslant 20} \\ {{\text{deformation }}{p_8} \leqslant 1.9} \end{array}} \right. (7) 式中:f(P) 为优化目标函数,P为多个截面参数的集合;p1为轿底底板厚度的集合;p2为直梁槽钢高度的集合;p3为上梁槽钢高度的集合;p4为直梁连接件槽钢高度的集合;p5为下梁槽钢高度的集合;p6为轿底底架槽钢高度的集合;p7为拉杆半径的集合;p8为模型最大变形量。
设置上述优化模型后开始计算,逐步生成样本点。经过20次迭代计算后,计算过程停止,共得到130个样本点。Workbench自动选取了其中三组结果较好的候选样本点(表4),其中第3组样本点不符合轻量化的设计目标。因此,针对第1组和第2组候选点(分别称为方案1和方案2)的输入参数(轿底底板的厚度皆为8 mm,拉杆半径皆为15 mm)进行选型,具体型号见表5。
表 4 候选点样本候选点 第1组 第2组 第3组 轿底底板厚度/mm 8.000 0 8.113 5 11.686 0 直梁槽钢高度/mm 50.00 105.42 206.01 上梁槽钢高度/mm 315.16 266.50 316.82 直梁连接件槽钢高度/mm 149.140 154.590 85.333 下梁槽钢高度/mm 274.56 299.72 197.63 轿底底架槽钢高度/mm 50.000 69.873 183.990 拉杆半径/mm 14.840 15.179 17.940 模型最大变形量/mm 1.892 1 1.802 2 1.401 8 轿架质量/kg 2 598.8 2 757.4 3 984.3 表 5 优化后模型构件型号模型构件 型号 方案1 方案2 直梁 5B 10B 上梁 32B 27B 直梁连接件 14B 16B 下梁 27B 30B 轿底底架 5B 6.3B 4.4 轿架优化结果对比与分析
通过对轿架模型的直接优化求解,获得了各构件的参数以及轿架的最大变形量和质量的候选点,但求解得出的构建参数并非实际槽钢的尺寸参数,只能作为参考值。因此,需要按照候选点选型设计中的方案重新进行力学校核。
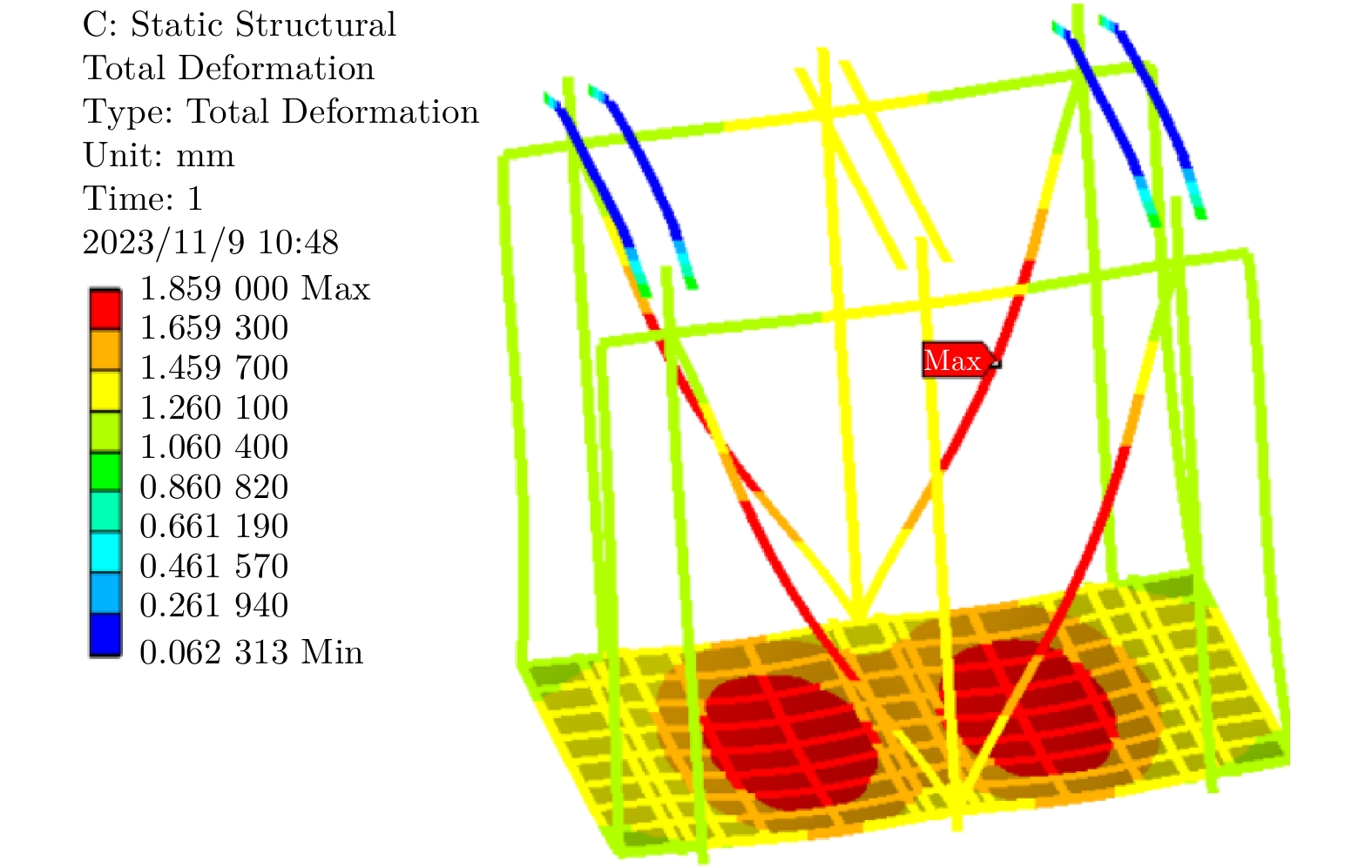
按照标准及优化方案1和方案2分别进行超载和偏载的静刚度分析以及模态分析。施加与初始轿架模型分析相同的载荷和约束条件,其中方案2的超载静刚度分析结果如图9和图10所示。
按照优化方案1对各个构件赋予相应的截面参数后,最终整个轿架模型的质量为2 531.7 kg,在原模型质量3 200 kg的基础上,质量降低了20.7%,取得了较好的轻量化效果。从静力学求解结果可以看出,方案1在变形和应力略微增加的基础上(在要求范围内),轻量化效果显著。
按照优化方案2对各个构件赋予相应的截面参数后,最终整个轿架模型的质量为2 658.5 kg,在原模型质量3 200 kg的基础上,质量降低了16.9%,取得了较好的轻量化效果。从静力学求解结果可以看出,与初始轿架模型相比,方案2模型的变形和应力略有增加,但都在要求的范围内。由模态分析的结果可知,前两阶模态频率有所降低,但对应的变形在原模型基础上也有明显的改善。
与方案1相比,方案2在变形和应力方面表现更好,集中变形区域和集中应力都更为均匀,其质量也只比方案1增加了126.8 kg。因此,方案2在变形和应力略微增加的基础上(在要求范围内),轻量化的效果明显,并且强度和刚度更能满足要求。
5. 结束语
本文通过静载、动载与模态分析,系统评估了大吨位货梯轿架结构的力学性能,确定轿厢底与拉杆为最大变形区域。原设计冗余度高,轻量化潜力大,为后续拓扑优化与尺寸优化提供了数据支撑。通过拓扑优化与尺寸优化相结合的方法,实现了大吨位货梯轿架结构的轻量化设计。优化后,轿架质量显著降低,其中方案1降低了20.7%,方案2降低了16.9%,同时力学性能满足强度与刚度要求。
文中提出离散型参数拟合方法以提升尺寸优化的效率,建立装配尺寸关联模型以确保优化后构件的兼容性,并通过多工况分析验证优化结构的鲁棒性。结果表明,优化方案2在质量与性能间取得更优的平衡,其应力分布均匀性及模态特性优于原设计,为实际工程应用提供了可靠依据。
本文对大吨位货梯进行尺寸与拓扑优化,实现了其轻量化设计,但仍有以下不足:
1) 本文得出的拉杆拓扑优化模型是将单一工况下的两个拓扑优化结果相结合得出的新拉杆结构布局,但在实际中应考虑几种工况共存下的拓扑优化;
2) 虽对货梯轿架模型进行了结构轻量化技术研究,在模型分析中取得了较好的效果,但因受限于项目阶段与资源条件,暂未开展实物样机实验验证。未来需结合动态加载测试与疲劳试验,量化优化模型的工程适用性,并基于实测数据修正仿真边界条件,以完善轻量化设计的可靠性验证体系。
-
表 1 Q235材料属性
密度/(kg·m−3) 屈服极限/MPa 杨氏模量/GPa 泊松比 7 850 235 210 0.3 表 2 力学分析结果
工况 最大
变形量/mm最大
应力 / MPa最大应力位置 超载 1.910 19.780 直梁和连接件连接处 偏载 1.870 20.690 直梁和连接件连接处 极限偏载 1.967 14.898 直梁和连接件连接处 冲击载荷 2.610 6.510 直梁和连接件连接处 安全制停 2.198 23.860 直梁和连接件连接处 表 3 六阶模态参数信息
阶次 频率/Hz 变形/mm 1 13.284 5.224 2 13.989 16.160 3 13.999 16.940 4 14.076 16.900 5 14.078 18.810 6 14.090 16.600 表 4 候选点样本
候选点 第1组 第2组 第3组 轿底底板厚度/mm 8.000 0 8.113 5 11.686 0 直梁槽钢高度/mm 50.00 105.42 206.01 上梁槽钢高度/mm 315.16 266.50 316.82 直梁连接件槽钢高度/mm 149.140 154.590 85.333 下梁槽钢高度/mm 274.56 299.72 197.63 轿底底架槽钢高度/mm 50.000 69.873 183.990 拉杆半径/mm 14.840 15.179 17.940 模型最大变形量/mm 1.892 1 1.802 2 1.401 8 轿架质量/kg 2 598.8 2 757.4 3 984.3 表 5 优化后模型构件型号
模型构件 型号 方案1 方案2 直梁 5B 10B 上梁 32B 27B 直梁连接件 14B 16B 下梁 27B 30B 轿底底架 5B 6.3B -
[1] 高晟, 李伟, 杨毅, 等. 有限元分析在提升输送机轿厢结构优化上的应用[J]. 机械工程与自动化, 2016(1): 68−70. DOI: 10.3969/j.issn.1672-6413.2016.01.029 [2] 王亮, 周晗, 简显科, 等. 特大载重货梯轿厢结构设计与轻量化[J]. 工程机械, 2022, 53(4): 46−51. DOI: 10.3969/j.issn.1000-1212.2022.04.009 [3] 洪睿. 曳引驱动乘客电梯能耗测量及能效评定方法的研究[D]. 杭州: 浙江大学, 2018. [4] 夏艳光, 夏崇俊, 许迪. 电梯轿厢架轻量化的分析研究[J]. 节能, 2012, 31(1): 63−66. DOI: 10.3969/j.issn.1004-7948.2012.01.016 [5] 邹玉静. 针对电梯结构强度的CAE分析[J]. 起重运输机械, 2007(11): 59−61. DOI: 10.3969/j.issn.1001-0785.2007.11.020 [6] AYTAC O, ERDEM İ. Reliability analysis of elevator car frame using analytical and finite element methods[J]. Building Services Engineering Research & Technology, 2012, 33(3): 293−305.
[7] 姜程. 曳引电梯轿架力学性能分析及结构优化[D]. 广州: 华南理工大学, 2020. [8] 余琛. 基于参数化水平集的结构多尺度拓扑优化方法研究[D]. 武汉: 华中科技大学, 2022. [9] 李照阳. 主动航天服关节助力外骨骼机器人关键技术研究[D]. 成都: 电子科技大学, 2022. [10] 白建涛. 考虑制造约束的薄壁结构优化设计与应用[D]. 吉林: 吉林大学, 2021.





 下载:
下载: